Tin Tức Chung
2 tam giác đồng dạng khi nào? Các trường hợp 2 tam giác đồng dạng
Chuyên đề về 2 tam giác đồng dạng trong chương trình Toán 8 là một phần kiến thức vô cùng quan trọng. Và trong bài viết hôm nay, chonmuamay.com sẽ hệ thống lại tất cả những kiến thức cần ghi nhớ về tam giác đồng dạng, hãy cùng theo dõi nhé!
Contents
2 tam giác đồng dạng là gì?
Hai tam giác đồng dạng là hai tam giác có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Tam giác ABC và tam giác A’B’C’ được gọi là đồng dạng với nhau
khi: A = A’; B = B’; C = C’ và và A′B′AB=B′C′BC=A′C′AC
Kí hiệu hai tam giác đồng dạng với nhau: △ABC∼△A′B′C′
Tỉ số: A’B’AB = B’C’BC = A’C’AC = k được gọi là tỉ số đồng dạng
Các trường hợp 2 tam giác đồng dạng của tam giác thường
Trường hợp 1: Cạnh – cạnh – cạnh (c-c-c)
Trong trường hợp này hai tam giác đồng dạng với nhau khi ba cạnh của tam giác này bằng ba cạnh của tam giác kia. Đối với trường hợp này chúng ta sẽ không cần phải so sánh giá trị góc của hai tam giác với nhau.
Cho hai tam giác ABC và tam giác A’B’C’ đồng dạng với nhau thì:
AB = A’B’; BC = B’C’; AC = A’C’
Trường hợp 2: Góc – góc (g-g)
Hai tam giác được gọi là hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh của chúng tương ứng bằng nhau.
Ví dụ: Cho tam giác ABC và tam giác A’B’C’, ta có:
- A= A’
- B= B’
=> △ A’B’C’ đồng dạng với △ ABC
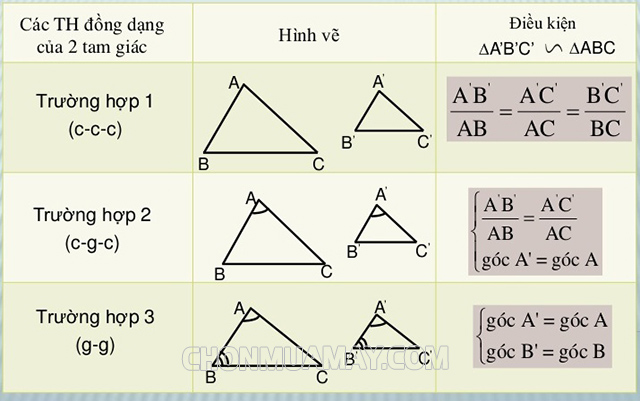
Trường hợp 3: Góc – cạnh – góc (g-c-g)
Trong trường hợp góc – cạnh- góc này thì hai tam giác được coi là hai tam giác đồng dạng với nhau khi hai góc và cạnh bên của cả hai tam giác đó bằng nhau.
Hoặc chúng ta có thể hiểu rằng, trường hợp này là hai tam giác đồng dạng khi hai cạnh có tỉ lệ bằng nhau và góc xen giữa hai cạnh của hai cạnh bằng nhau.
Ví dụ: Xét hai tam giác ABC và tam giác A’B’C’ đồng dạng với nhau khi:
ABA’B’ = ACA’C’
A = A’
=> Tam giác A’B’C’ đồng dạng với tam giác ABC
Các định lí 2 tam giác đồng dạng trong tam giác vuông
- Định lí 1: Nếu cạnh huyền và cạnh góc góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau
- Định lí 2: Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau
- Định lí 3: Nếu góc nhọn của hai tam giác bằng nhau thì hai tam giác vuông đó là hai tam giác đồng dạng
Tổng hợp các phương pháp chứng minh 2 tam giác đồng dạng toán lớp 8
Phương pháp 1: Hai tam giác được coi là đồng dạng nếu chúng có các cặp cạnh tương ứng tỉ lệ và các góc tương ứng tỉ lệ.
Phương pháp 2: Định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó vạch ra trên cạnh đó những đoạn thẳng tương ứng tỷ lệ.
Phương pháp 3: Chứng minh các điều kiện cần và đủ để hai tam giác đồng dạng: Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng. Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng. Hai tam giác có hai cặp cạnh tương ứng tỷ lệ, hai góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng.
Phương pháp 4: Chứng minh trường hợp 1 (cạnh-cạnh-cạnh): Nếu 3 cạnh của tam giác này tỷ lệ với 3 cạnh của tam giác kia thì 2 tam giác đó đồng dạng.
Phương pháp 5: Chứng minh trường hợp 2 (cạnh-góc-cạnh): Nếu 2 cạnh của tam giác này tỷ lệ với 2 cạnh của tam giác kia và 2 góc tạo bởi tạo các cặp cạnh đó bằng nhau thì hai tam đó giác đồng dạng.
Một số bài tập về 2 tam giác đồng dạng
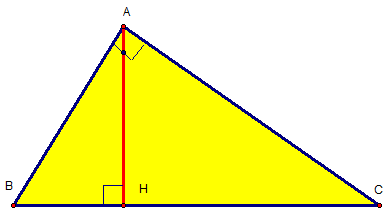
Bài 1: Cho tam giác ABC vuông tại A, có đường cao AH.
Chứng minh các hệ thức:
- a) AB2= BH.BC và AC2= CH.BC
- b) AB2 + AC2 = BC2
- c) AH2 = BH.CH
- d) AH.BC = AB.AC
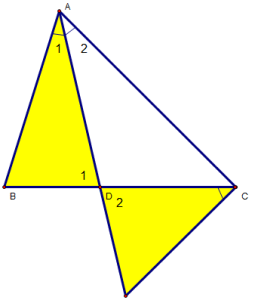
Giải:
- a) Xét hai ∆ABC và ∆ HAC, ta có: AC2= CH.BC
BAC = AHC = 900
C là góc chung
=> ∆ABC ~ ∆HAC (g – g)
=> ACHC = BCAC
=> AC2= CH.BC (1)
Chứng minh tương tự, ta có: AB2= BH.BC (2)
- b) AB2 + AC2 = BC2
Từ (1) và (2) ta có:
AB2 +AC2 = BH.BC + CH.BC = (BH+CH).BC = BC2
- c) AH2 = BH.CH
Xét hai ∆HBA và ∆ HAC, ta có:
BHC=AHC = 90O
ABH = HAC cùng phụ BAH
=> ∆HBA ~ ∆HAC (g – g)
=> HAHC = HBHA
=> AH2 = BH . CH
AH.BC = AB.AC
Ta có:
HAAB = ACBC (∆ABC ~ ∆HAC)
⇒ AH.BC = AB.AC
Bài 2: Cho ∆ABC nhọn. kẻ đường cao BD và CE. vẽ các đường cao DF và EG của ∆ADE.
Chứng minh:
- a) ∆ABD đồng dạng ∆AEG
- b) AE = AB.AG = AC.AF
- c) FG // BC
Giải:
- a) xét ∆ABD và ∆AEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
⇒ BD // EG
⇒ ∆ABD ~ ∆AGE
- b) => ABAE = ADAG
⇒ AD.AE = AB.AG (1)
Chứng minh tương tự, ta được: AD.AE = AC.AF (2)
Từ (1) và (2) suy ra: AD.AE = AB.AG = AC.AF
- c) Xét ∆ABC, ta có:
AB.AG = AC.AF (cmt)
ABAF = ACAG
⇒ FG // BC (định lí đảo talet)
Trên đây, chonmuamay.com đã tổng hợp tất tần tật những kiến thức liên quan đến 2 tam giác đồng dạng. Hy vọng bài viết đã mang đến cho các bạn những kiến thức hữu ích!
