Công thức tính thể tích khối nón, hình nón cụt và bài tập vận dụng

Để giúp bạn đọc hiểu hơn về khối nón cũng như cách tính thể tích khối nón, danhgiamay.com xin gửi đến các bạn bài viết dưới đây. Đồng thời, cung cấp đến các bạn một số bài tập vận dụng từ cơ bản đến nâng cao! Hãy cùng theo dõi nhé!

Ảnh đại diện

Công thức tính thể tích khối nón 

Thể tích khối nón được tính bằng ⅓ tích của số pi, chiều cao và bình phương bán kính đáy của hình nón.

V= 1/3.B.h = 1/3.r².h

Trong đó:

• • • V là thể tích hình nón
    • là hằng số ( = 3,14)
    • r là bán kính đáy hình tròn
    • h là chiều cao của hình nón

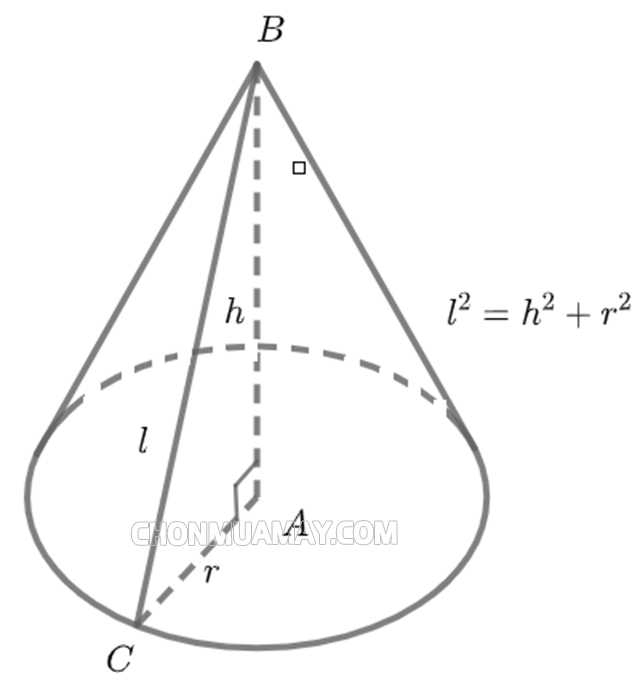
Công thức tính thể tích khối nón tròn xoay

Công thức tính thể tích của khối nón tròn xoay cũng tương tự công thức tính thể tích khối nón, được tính bằng ⅓ tích của số pi, chiều cao và bình phương bán kính đáy của hình nón.

V= 1/3Bh = 1/3.r².h

Trong đó:

• • • V là thể tích hình nón
    • là hằng số ( = 3,14)
    • r là bán kính đáy hình tròn
    • h là chiều cao của hình nón

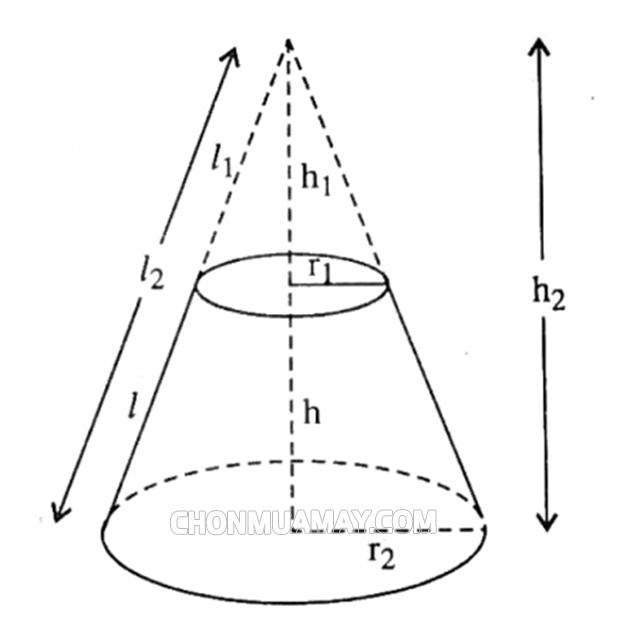
Công thức tính thể tích khối nón cụt

Thể tích hình nón cụt bằng hiệu thể tích của hình nón lớn và hình nón nhỏ

V= 1/3(r1² + r2²+ r1.r2).h

Trong đó:

• • • V là thể tích hình nón cụt
    • r1, r2 là bán kính 2 đáy của hình nón cụt
    • h là chiều cao của hình nón cụt (khoảng cách giữa 2 đáy)

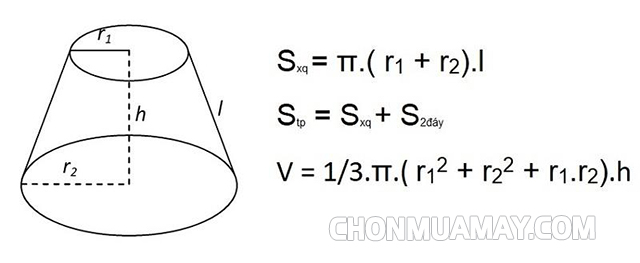
Bài tập về công thức tính thể tích hình nón 

Bài tập 1:

Cho hình nón có đỉnh là O, có độ dài đường sinh bằng 5cm, bán kính hình tròn đáy bằng 3cm. Tính thể tích khối nón.

Bài giải: 

Gọi O là đỉnh của khối nón

H là tâm của hình tròn

A là điểm thuộc đường tròn đáy

Theo đề bài, ta có:

OA=5cm, HA=3cm

Áp dụng định lý Pytago vào tam giác vuông OHA, ta tính được độ dài OH:

OH= √(OA²- HA²)= √(5²- 3²) = 4

V = 1/3.π.R².h = 1/3.3².4=12π(cm³)=37,68(cm³)

Vậy thể tích của khối nón là 37,68 cm3

Bài tập 2:

Cho một hình nón cụt có bán kính hai mặt đáy r1 và r2 lần lượt bằng 5cm và 9cm. Chiều cao nối giữa hai bán kính mặt đáy này có độ dài 8cm. Hỏi diện tích toàn phần của hình nón này bằng bao nhiêu?

Bài giải:

Áp dụng theo công thức tính thể tích hình nón cụt ta có:

r1 = 5cm, r2 = 9cm, h = 8cm

V = 1/3π.8. (52 + 5.9 +92) = 1264,37 (cm3)

Như vậy thể tích của hình nón cụt này bằng 1264,367 cm3

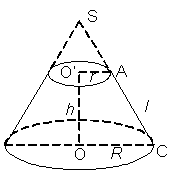
Bài tập 3:

Người ta đã cắt hình nón bằng một mặt phẳng (Q) song song với đáy và đi qua trung điểm của đường cao hình nón đó, tạo thành một hình nón cụt. Hãy tính thể tích của hình nón cụt đó? Có R= 5cm, Sxq= 65π cm

Bài giải: 

Áp dụng công thức tính diện tích đáy của hình nón, ta có:

Sđáy= πR²= π.5²=25π(cm2)

Dựa vào công thức tính diện tích xung quanh chúng ta suy ra được cách tính đường sinh của hình nón, cụ thể:

l= Sxq/πR=65π/5π=13(cm2)

Gọi đường cao của hình nón là SO, ta có:

SO=√(SC²-OC²)= √(13²- 5²)= 12 (cm2)

Từ đó, chúng ta có thể tích hình nón là:

V= 1/3.π.5².12 = 100π(cm3)

Gọi O’ là trung điểm của SO

Gọi A là giao điểm của SC với mặt phẳng (Q)

Vì O’A là đường trung bình của tam giác SOC nên O’A=2,5(cm)

Vậy thể tích của hình nón cụt đó là:

V= 1/3.π.6.(5²+ 2,5²+ 5.2,5)=87,5π (cm³)

Bài tập 4:

Cho hình nón cụt có đường kính hai mặt đáy lần lượt là 12cm và 18cm. Chiều cao nối giữa hai mặt đáy có độ dài 7 cm. Tính thể tích hình nón cụt đó!

Bài giải: Theo đề ra, ta có đường kính của 2 mặt đáy lần lượt là: 12cm và 16cm.

Vậy bán kính đáy sẽ bằng:

r1=12/2=6(cm)

r2=18/2=9(cm)

h=7(cm)

Áp dụng công thức tính thể tích hình chóp cụt 

V=1/3.π.(r1²+r2²+r1.r2)h

=> V=1/3.π.(6²+9²+6.9).7= 1253,5π(cm3)

Bài tập 5:

Cho hình nón N có góc ở đỉnh bằng 60 độ, mặt phẳng qua trục của hình nón và cắt hình nón theo một thiết diện là tam giác có bán kính đường tròn ngoại tiếp tam giác bằng 2. Hãy tính thể tích khối nón N.

Bài giải: Trong tam giác SAB đều, ta có SA=SB và góc S bằng 60 độ. Tâm đường tròn ngoại tiếp của tam giác SAB là trọng tâm của tam giác.

Ta có bán kính đường tròn ngoại tiếp tam giác SAB là:

r=2/3.SO=2 <=>  SO= 3

Mà SO= SA.sin60°.SA= SO.sin60°= 3/(√3/2) = 2√3

Vậy bán kính của đường tròn khối nón là:

R=AB/2=2√3/2= √3

Áp dụng công thức tính thể tích khối nón, ta có:

V= 1/3.π.(√3)².3 = 3π = 9.42(cm3)

Bài viết trên đây, chonmuamay.com đã chia sẻ đến các bạn công thức tính thể tích khối nón và các bài tập minh họa. Hy vọng các bạn sẽ hiểu và áp dụng tính thể tích hình nón chuẩn nhất. Chúc các bạn thành công!